« mtrlzng I » | Tomohiro TACHI | 舘知宏

舘知宏 『フリーフォーム・オリガミ』
素材:1,100mm×1,300mm Stainless Steel Sheet
—
折りで表面を覆い尽くすことにより、正・負のガウス曲率を持つ自由曲面形状を零ガウス曲率曲面=折紙で実現した。本手法は一般の曲面に拡張され得る。あらゆる曲面が板の折りと曲げのみで形作ることが可能である。
本作品は作者が開発するFreeform Origami システムの試験モデルとして製作された。Freeform Origami システムは、折紙の数理に基づき、製作可能な折紙形状の解空間をインタラクティブに探索可能とする。
[essay: 情報と物質とそのあいだ]
折紙は一枚の平面領域を伸び縮みさせず切り貼りしない、という幾何拘束(等長埋め込み)のもとで変形させ、得られる形の解空間である。このような制約条件は、ともすると自由な造形を妨げる要因であると考えられがちだが、解き方次第では、豊かな見立て・連想の多様性を生む。ゆえに、幾何拘束こそ折紙の造形の本質といってもよい。さらにいえば、幾何拘束はあらゆる造形の本質である。なぜなら、拘束が無く可能性のすべてが保証されている状態を仮定するなら、それは認識の手がかりの無いノイズとなってしまうからである。
このような折紙の幾何拘束は論理的に記述可能な問題であるから、適切なアルゴリズムによって解くことができる。これらを扱う研究領域はコンピュテーショナル・オリガミと呼ばれる。一方で、あたりまえだが、折紙は紙というマテリアルの物理世界における挙動そのものを扱う。紙という極度に薄くて硬い材料に圧縮力をかけたときの座屈現象は微分不連続な形状を作る。平たく言えば,紙をくしゃくしゃにすると「クシャクシャ」という音を立て、折り目を形作る。ここで起きた現象を、「紙というマテリアルが等長写像という幾何の問題とそれを解くための計算システムを内包しており、紙をくしゃくしゃにする行為によって計算が実行された」と解釈する。こうすると、ある物理現象を記述するにはどのようなアルゴリズムが必要かという問題に対して、あるアルゴリズムを与えたときに、それを実行するためにはどのような物理現象が必要か、という逆問題を思考することができる。この逆問題は、計算された形を物質化するというだけではなく「問題とそのアルゴリズム自体を物質化する」という「システムのマテリアリゼーション」の問題でもある。
[略歴] (2013/06)
2005年東京大学建築学科卒業,2010年同大学院工学系研究科博士課程修了。博士(工学)。現在,東京大学大学院総合文化研究科助教。東京藝術大学非常勤講師。RGSS共同主催。
折紙の数理研究・計算に基づく設計手法の研究・システム開発を行う。折紙作家。
[主な作品]
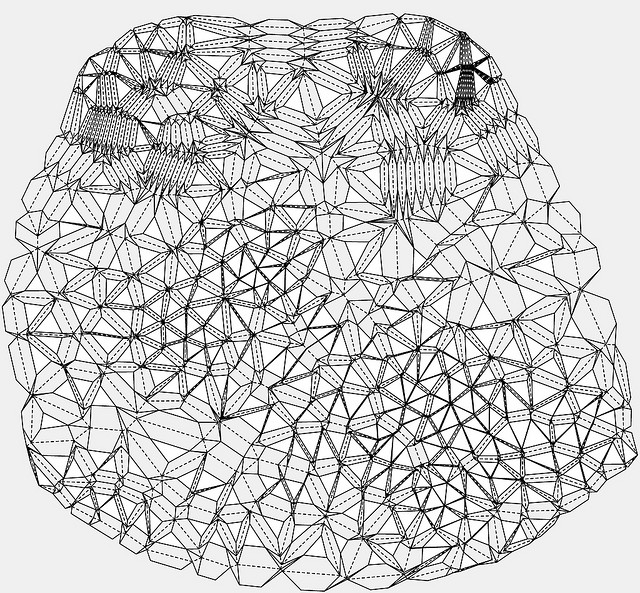

「Stanford Bunny」
「建築折紙」 2010年NTTインターコミュニケーション・センター「可能世界空間論」にて展示
「Free Form Origami」 折り紙の展開図と折られた形状をインタラクティブにシミュレーションするソフトウェア
